|
The Kruskal-Wallis test is a distribution free (nonparametric) alternative to ANOVA. It compares several samples and tests the hypothesis:
H0 the samples are all drawn from populations that have equal means
H1 the mean of at least one of the populations is different
The test involves:
- sort the combined results into size order and allocate ranks
- form a table that contains the ranks, instead of the values
- calculate the test statistic 'K using the formula:
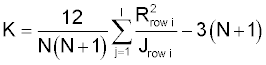
Where:
| Ri |
sum of the ranks in row 'i' |
| J |
number of values in row 'i' |
| I |
number of rows |
| N |
total number of values |
'K' has an approximately χ 2 distribution with degrees of freedom I - 1
|