|
Cohen's kappa is used to compare the degree of consensus between raters (inspectors) in, for example, Measurement Systems Analysis. It uses a contingency table approach.
Two raters inspect 150 parts independently and make the following determinations:
| |
|
|
Bret
|
|
| |
|
Reject
|
Accept
|
Total
|
| |
Reject |
20
|
19
|
39
|
| Alice |
Accept |
1
|
110
|
111
|
| |
Total |
21
|
129
|
150
|
The expected values in each cell would be:
| |
|
|
Bret
|
|
| |
|
Reject
|
Accept
|
Total
|
| |
Reject |
5.46
|
33.54
|
39
|
| Alice |
Accept |
15.54
|
95.46
|
111
|
| |
Total |
21
|
129
|
150
|
These are the values that would give the same totals if the determinations were made by pure chance and is calculated from:
(row total x column total)/overall total
The Kappa statistic is calculated from:
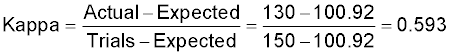
where:
| Actual |
the number of times the appraisers agreed (110 + 20 = 130) |
| Expected |
the number of times they would have agreed by chance (5.46 + 95.46) |
| Trials |
the number of trials |
The value of Kappa will be between 0 and 1.
If the results were made by chance, neither rater showing judgment the value would be zero. If the raters were in perfect agreement, the number of agreements would equal the number of trials and Kappa would be 1.
|