The variance is a measure of the process variation. The greater the scatter of the data values, the larger the variance. The variance is the average distance of the data values from the mean.
More precisely the variance is the mean of the squares of the distance of the data values from the mean:
|
|
|
i
|
 |
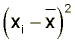 |
|
1
|
-3
|
9
|
|
2
|
-2
|
4
|
|
3
|
-1
|
1
|
|
4
|
+2
|
4
|
|
5
|
+4
|
16
|
|
Sum
|
0
|
34
|
|
|
Variance
|
8.5*
|
|
The values are squared because the square of any value is positive. Notice that if we used:
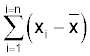
some of the values would be negative and others positive, the sum of all the values is zero. Squaring makes all the values positive and is a convenient way of overcoming this.
You will notice that to calculate the average we divided by 'n-1' rather than 'n' as you might expect. If you knew the process mean you would use the formula:
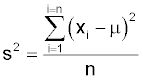
However you do not normally know the parameter μ and so you substitute x-bar. You use the sample values to calculate x-bar and then you reuse them to calculate the variance. This gives the value of s2 a bias which can be removed by dividing by 'n-1' and the formula becomes:
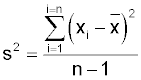
The statistic x-bar is an unbiased estimate of μ. It is an estimate based on a small sample so it is unlikely to exactly equal μ but it is equally likely to be too big or too small. You might expect that using this approximation would make the estimate of the process variance less accurate, but you might not expect it to introduce a bias.
We know that:
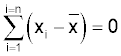
A consequence of this (which I won't prove) is that you could not substitute any value for x-bar that would give a smaller value to the equation:
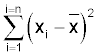
Thus any difference between x-bar and the true value of μ will always reduce the estimate of s2. The estimate of s2 is biased but it turns out that dividing by 'n-1' instead of 'n' exactly compensates for this bias.
The reason for this is that because we originally calculated x-bar from the same xi values the data values and the value of x-bar are not independent of each other. If you know any 'n-1' data values then you can calculate the missing value.
This is a specific example of an important concept in statistics known as the number of 'Degrees of Freedom'. The number of degrees of freedom is the number of independent data values in the equation.
The number of degrees of freedom is the number of data values you need to know to calculate the remaining values if you know the values of any statistics used in the formula.
In more advanced statistics you will come across examples where you might find it difficult to work out how many degrees of freedom there are. It will help greatly if you bear this rule in mind.
 |
The average of the five values is 7, find the missing value, X5:
|
|
|