Histograms are an excellent way of showing the variation graphically. However if we are to compare processes and evaluate improvements or changes objectively we need a hard number.
The measure that is almost invariably chosen is the 'standard deviation'. It is easiest to start by explaining the variance, which is just the square of the standard deviation.
I'll explain how to calculate it first and then explain how it works. The process variance is a parameter represented by the Greek symbol 'σ 2' (sigma squared). We cannot calculate this directly but instead use the statistic 's2' calculated from a sample as an estimate:
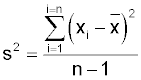
Notice that it uses similar notation to the formula for the mean. It looks more forbidding and Ill go through the calculation with a small sample of numbers:
The mean is 4:
|
1) The Index
|
2) The Data
|
3) The Mean
|
4) The difference between the data values and the mean
|
5) The square of column (4)
|
|

|

|

|

|

|
|
1
|
1
|
4
|
-3
|
+9
|
|
2
|
2
|
4
|
-2
|
+4
|
|
3
|
3
|
4
|
-1
|
+1
|
|
4
|
6
|
4
|
+2
|
+4
|
|
5
|
8
|
4
|
+4
|
+16
|
| |
|
|

|
34
|
There are five data values 'n'. The variance is obtained by dividing by 'n-1'

 |
The times taken to repair equipment breakdowns, in hours, over the past week were as follows:
What was the variance of the repair time?
|
|
|