|
In a Taguchi design, the name used for the design array that contains the controllable factors, as opposed to the Outer Array that contains the noise factors. See Outer Array for a more complete description.
Linear graphs are used to help allocate the appropriate columns of a Taguchi array to the factors and interactions. The figures show two alternative linear graphs for the L8 design:
Column 3 contains the interaction between columns 1 and 2.
Column 1 contains few sign level changes.
The circles are coded to distinguish the columns that have many level changes from those with few changes. If it is difficult to change the level of one of the factors, column 1 would be a good choice, and column 4 a poor choice (Taguchi designs are not usually randomized).
See Taguchi Loss Function
Taguchi distinguishes between 'noise' factors and 'controllable' factors. Noise factors are those that cannot be controlled in normal operation, but can be controlled for the purpose of testing. An example is shown below. The experiment is to find the best values for the three design features in a relief valve: Hole Size, Spring Length and Ball Size. The noise factors are the Oil Temperature and Water Vapor Pressure.
|
|
Outer Array
|
|
D Oil Temperature
|
1
|
2
|
1
|
2
|
|
|
E Water Vapor Pressure
|
1
|
1
|
2
|
2
|
|
| |
Inner Array
|
|
|
|
|
|
| |
A (hole)
|
B (spring)
|
AB
|
C (ball)
|
AC
|
BC
|
-
|
|
|
|
|
|
|
Run
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
|
|
|
S/N Min
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
44.9
|
51.9
|
52.6
|
59.9
|
-34.42
|
|
2
|
1
|
1
|
1
|
2
|
2
|
2
|
2
|
102.0
|
113.5
|
125.0
|
99.0
|
-40.86
|
|
3
|
1
|
2
|
2
|
1
|
1
|
2
|
2
|
47.3
|
51.3
|
54.1
|
61.1
|
-34.60
|
|
4
|
1
|
2
|
2
|
2
|
2
|
1
|
1
|
111.0
|
103.0
|
104.0
|
127.5
|
-40.97
|
|
5
|
2
|
1
|
2
|
1
|
2
|
1
|
2
|
157.8
|
157.2
|
154.3
|
165.2
|
-44.01
|
|
6
|
2
|
1
|
2
|
2
|
1
|
2
|
1
|
188.5
|
194.0
|
211.5
|
197.5
|
-45.94
|
|
7
|
2
|
2
|
1
|
1
|
2
|
2
|
1
|
148.6
|
159.5
|
198.0
|
176.7
|
-44.70
|
|
8
|
2
|
2
|
1
|
2
|
1
|
1
|
2
|
220.0
|
198.5
|
217.5
|
220.0
|
-46.62
|
| S/N avg @ 2 |
-45.31
|
-41.72
|
-41.38
|
-43.59
|
-42.63
|
-41.52
|
-41.52
|
|
|
|
|
|
| S/N avg @ 1 |
-37.71
|
-41.31
|
-41.65
|
-39.43
|
-40.39
|
-41.50
|
-41.51
|
|
|
|
|
|
| D S/N |
-7.60
|
-0.41
|
0.27
|
-4.16
|
-2.24
|
-0.02
|
-0.01
|
|
|
|
|
|
A robust process is one that is insensitive to variation and thus gives consistent quality. The Taguchi approach is aimed at achieving robust processes by finding the 'dispersion factors'.
Taguchi proposed using 'Signal to Noise' ratios to optimize processes. The idea is that the best process settings are those that maximize the signal to noise ratio.
If the requirement is to [maximize/minimize] the response then maximizing the signal to noise ratio may not achieve the [highest/lowest] value that can be attained if process variation is ignored. It does however give the [highest/lowest] average value when variation is taken into account.
If the requirement is to achieve a target response, maximizing the signal to noise ratio will give the factor settings that achieve the target response with least variation. The signal to noise ratios are:
|
Minimize the Response
|
Maximize the Response
|
Achieve a Target
|
|
|
|
|
Taguchi developed a series of arrays for use with Taguchi Designs. These are designated Ln arrays, where 'n' is the number of runs.
The columns in these arrays are highly confounded. They are generally used as screening designs, with only selected interactions investigated. A feature of these arrays is that the two way interactions have the signs reversed; if A and B are both +1, then AB would be -1. The arrays include two, three, four, and mixed level designs.
Taguchi designs are a type of experimental design pioneered by Genichi Taguchi. They are distinguished by the use of:
- the Signal to Noise Ratio
- inner and outer arrays
- Taguchi arrays
The analysis focuses on graphical, rather than analytical methods.
Taguchi challenged the view that anything within specification was good product, and needed no action. He asserted that any deviation from the target was a 'loss to society' in reduced life expectation, utility etc.
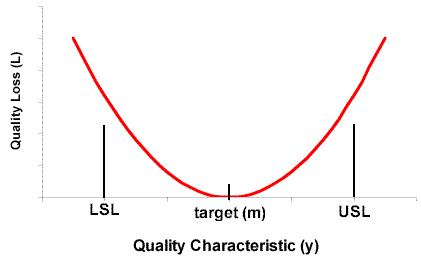
He proposed that the loss function could be represented by a quadratic where:
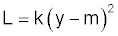
For the process output this gives:
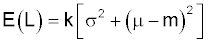
|