|
Friedman's Test is a nonparametric alternative to two-way analysis of variance. The hypothesis is:
H0 the means of all the samples are equal
H1 the mean of at least one of the samples is different
Consider the example where three treatments are evaluated on four different patients:
|
Therapy
|
Andrew
|
Belinda
|
Chris
|
Dave
|
| Relaxed |
110
|
140
|
100
|
130
|
| Normal |
115
|
150
|
105
|
135
|
| High Intensity |
117
|
155
|
100
|
135
|
The test involves:
- impose ranks on each of the columns. If values are equal, average the ranks they would have got if they were slightly different:
|
Therapy
|
Andrew
|
Belinda
|
Chris
|
Dave
|
| Relaxed |
1
|
1
|
1.5
|
1
|
| Normal |
2
|
2
|
3
|
2.5
|
| High Intensity |
3
|
3
|
1.5
|
2.5
|
- calculate the Fr statistic using the formula:
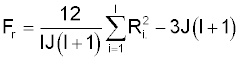
Where:
| I |
Number of samples (treatments) |
| J |
Number of blocks |
| Ri |
sum of the ranks in row 'i' |
This gives a value for Fr of 4.65
The value of Fr has an approximately chi-square distribution with I - 1 degrees of freedom.
This is a distribution free alternative to ANOVA. It will compare several samples and test the hypothesis:
H0 the means of all the samples are equal
H1 the mean of at least one of the samples is different
The test involves:
- sort the combined results into size order and allocate ranks
- form a table that contains the ranks, instead of the values
- calculate the test statistic 'K using the formula:
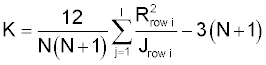
Where:
Ri sum of the ranks in row 'i'
J number of values in row 'i'
N the total number of values
I the number of rows
'K' has an approximately c2 distribution with degrees of freedom I - 1
The ANOVA method relies on the assumption that the variance is the same for all the samples. Levene's test is:
H0 the variance is the same for all the samples
H1 the variance of at least one of the samples is different
The test uses the statistic 'W' where:
Where:
| N |
total number of values |
| Ni |
number of values in row 'i' |
| k |
number of levels |
 |
median of level 'i' |
 |
the average of all the zij values |
 |
the average of the zij values in row 'i' |
This is the nonparametric version of the two sample t-test; it compares the means of two samples. It tests the hypothesis:
H0 the means are equal
H1 the mean of sample 'm' is [less than/greater than/not equal to] the mean of sample 'n'
It is similar in concept to the Wilcoxon Signed Rank Test and is also known as the Wilcoxon Rank Sum Test. The test involves:
- sort the combined results into size order and allocate ranks
- find the sum 'w' of the ranks of the sample with the smallest number of values (if they both have the same number of values, select either). This is one of the critical values.
For small data sets the critical value is found from published tables. Because the sum of the ranks must be an integer, it is not usually possible to find the exact critical value:
m is the number of values in the sample with the least number of values
n is the number of values in the other sample
m1 is associated with the sample containing the smallest number of values
See Mood's Median Test
The Mood's Median Test is a nonparametric equivalent of ANOVA. It is an alternative to the Kruskal-Wallace test. The hypothesis is:
H0 the medians of all the samples are equal
H1 the median of at least one of the samples is different
The test involves:
- find the median of the combined data set
- find the number of values in each sample greater than the median and form a contingency table:
| |
A
|
B
|
C
|
Total
|
|
Greater than the median
|
|
|
|
|
|
Less than or equal to the median
|
|
|
|
|
|
Total
|
|
|
|
|
- find the expected value for each cell:

- find the chi-square value from:
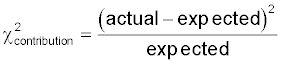
Most types of hypothesis tests require that the population conforms to a particular distribution, usually the normal distribution. Where this is not the case a nonparametric test can be used.
Nonparametric tests make no assumptions about the type of distribution (although they may require symmetry, or some other property). The disadvantage is that they are not as efficient; for a given data set the nonparametric test will give a higher p-value.
| Parametric Hypothesis Test |
|
A Parametric test make assumptions about the underlying distribution of the population from which the sample is being drawn, and which is being investigated. This is typically that the population conforms to a normal distribution.
Alternative name for Mood's Median Test
See the Mann Whitney Tests
| Wilcoxon Signed Rank Test |
|
This is the nonparametric equivalent of the one sample t-test. It tests the hypothesis:
H0 the mean equals zero
H1 the mean [is less than/greater than/not equal to] zero
The test involves:
- sort the values into order of their absolute magnitude (ignoring the signs) and allocate ranks
- calculate the sum the ranks of the data values are positive (S+)
An example would be:
| Rank |
1
|
2
|
3
|
4
|
5
|
6
|
| Data Value |
-1.0
|
-2.0
|
2.5
|
3.0
|
3.0
|
3.5
|
If the mean is non-zero the positive values will be clustered at one end or other of the ordered data set and S+ and S- will be very different.
For the example S+ = 3 + 4 + 5 + 6 = 18
For small data sets values the critical value is found from published tables. Because the sum of the ranks must be an integer, it is not usually possible to find the exact critical value:
For larger data sets the z-statistic can be found from:

This gives the upper tail test (the mean is less than zero). For the lower tail test, use the sum S+ and for the two tailed test use both, remembering to use the table value twice.
The p-value can be calculated using normal distribution tables.
|