In experimental design when two interactions, or a main effect and an interaction, share the same column, and so cannot be individually analyzed then their effects are aliased.
In the 23-1 design the factor C is aliased with the interaction AB:
|
Run
|
A
|
B
|
AB + C
|
|
1
|
-1
|
-1
|
+1
|
|
2
|
+1
|
-1
|
-1
|
|
3
|
-1
|
+1
|
-1
|
|
4
|
+1
|
+1
|
+1
|
Also Balanced Experiment. A factorial design in which each factor is run the same number of times at the high and low levels. Most factorial designs are balanced, unbalanced designs are only used in exceptional circumstances.
Blocking is a technique used to eliminate identified possible sources of variation that cannot be randomized. The experiment is organized into blocks, where the possible source of variation is held level in each block.
Suppose that there was insufficient material in one batch to carry out all the runs in an experiment. Half the runs could be done on one batch and half on another. The experiment would have to be carried out in such a way that the aggregate result was balanced between the two batches. At its simplest, if the experiment involved an even number of replications of each run then this would simply involve carrying out half the replications on one batch, and half on the other. Things are not usually so simple, and there are many ways of approaching more challenging situations.
In experimental design it is usual to substitute 'coded factors' for the actual physical values. In a factorial design the coded factors are given the levels '-1' and '+1'. This assists the analysis in various ways.
Factors or interactions are confounded when the design array is configured so that the effect of one factor is combined with the other. The effect of the individual factors/interactions cannot be isolated by the analysis.
Confounding is very similar to aliasing, although aliasing is used to describe factors/interactions that are fully confounded, rather than partially confounded.
The relationship that determines the aliasing structure in a design.
|
Run
|
A
|
B
|
AB + C
|
|
1
|
-1
|
-1
|
+1
|
|
2
|
+1
|
-1
|
-1
|
|
3
|
-1
|
+1
|
-1
|
|
4
|
+1
|
+1
|
+1
|
The Defining Relationship is I=ABC
When an experiment is conducted the variables manipulated by the experimenter are called "independent variables" or factors and the response or output variables are the "dependent variables".
The relationship used to create a fractional factorial design, and which creates the defining relation:
|
Run
|
A
|
B
|
AB + C
|
|
1
|
-1
|
-1
|
+1
|
|
2
|
+1
|
-1
|
-1
|
|
3
|
-1
|
+1
|
-1
|
|
4
|
+1
|
+1
|
+1
|
The Design Generator is A=BC
Experimental design involves conducting a systematic series of tests to discover the relationship between the factors effecting a process (X) and the critical outputs (responses). The inputs are varied in a systematic fashion and the effects on the response(s) are observed.
Used in experimental design to help select a fractional factorial design:
| Resolution III |
RIII |
two factor interactions are aliased with main effects |
| Resolution IV |
RIV |
two factor interactions are aliased with other two factor interactions, but not with main effects. Main effects are aliased with three factor interactions. |
| Resolution 5 |
RV |
two factor interactions are not aliased with each other, but are aliased with three factor interaction |
An RIII design would usually be used for screening experiments. There would rarely be any point in going beyond an RV design.
In general the resolution is the length of the shortest word in the defining relationship.
The degree to which data tend to spread about the mean. It is measured by the standard deviation, or variance.
Evolutionary Operation. An experimental design technique that involves making small changes to a process progressively, and during normal operation, to find the optimum operating conditions.
See Design of Experiments
An experimental design where the factor levels are specifically selected by the experimenter (cf. Random Effects Model)
See Dependent Variable for an explanation
In many processes the factors interact, the combined effect is not the sum of the individual effects. The figure below uses the well known danger of combining alcohol with some medications to illustrate the idea:
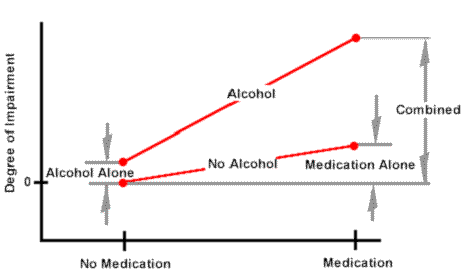
Interactions are an important consideration in experimental design.
The effect of a factor, as opposed to an interaction effect.
A design is orthogonal if each factor can be evaluated independently of all other factors. In a two level factorial design, this is achieved by matching each level of each factor with an equal number of each level of the other factors.
For example, in the array the '+1' level of Factor A (runs 2 and 4) is matched with one instance of Factor B at '-1' and one at '+1'. If any two columns are compared, the same thing will be found for both factor levels.
|
Run
|
A
|
B
|
AB + C
|
|
1
|
-1
|
-1
|
+1
|
|
2
|
+1
|
-1
|
-1
|
|
3
|
-1
|
+1
|
-1
|
|
4
|
+1
|
+1
|
+1
|
An experimental design where the factor levels are selected at random from a large number of possible levels. The analysis is based on the estimating variance.
This compares to a fixed effects model where a restricted number of levels are selected and set by the experimenter.
Experiments should be run in random order to randomize the effects of any variables that are varying during the experiment, and might impose a pattern on the results.
Randomizing destroys any systematic variation, which could not be detected by the analysis, and converts it to either 'common cause' variation, or variation that will be detected in the residual analysis.
Repeating the tests for each treatment. If each treatment is tested four times then there are four replications of the design.
An experimental design explores the effect of input factors on the process response. For example, an experiment might investigate the effects of altering the amounts of flour, water, yeast, oven temperature etc. on the consistency of bread. The consistency quality of the bread would be the response variable.
A desirable property of Response Surface Designs. It refers to designs where the variance is the same at all points that are the same distance from the design center.
A type of experimental design used when a large number of factors that may affect the process have been identified. The screening design is a Resolution III design identifies the factors that do not affect the process, so those remaining can be studied more closely.
Applying a mathematical operation to response data to make it conform to a normal distribution. Often necessary with experiments that involve rates because the results typically do not conform to a normal distribution.
Common transforms include natural log, reciprocal and squares.
A certain combination of factor levels whose effect on the response variable is of interest. Often replaced by the term 'run'.
|